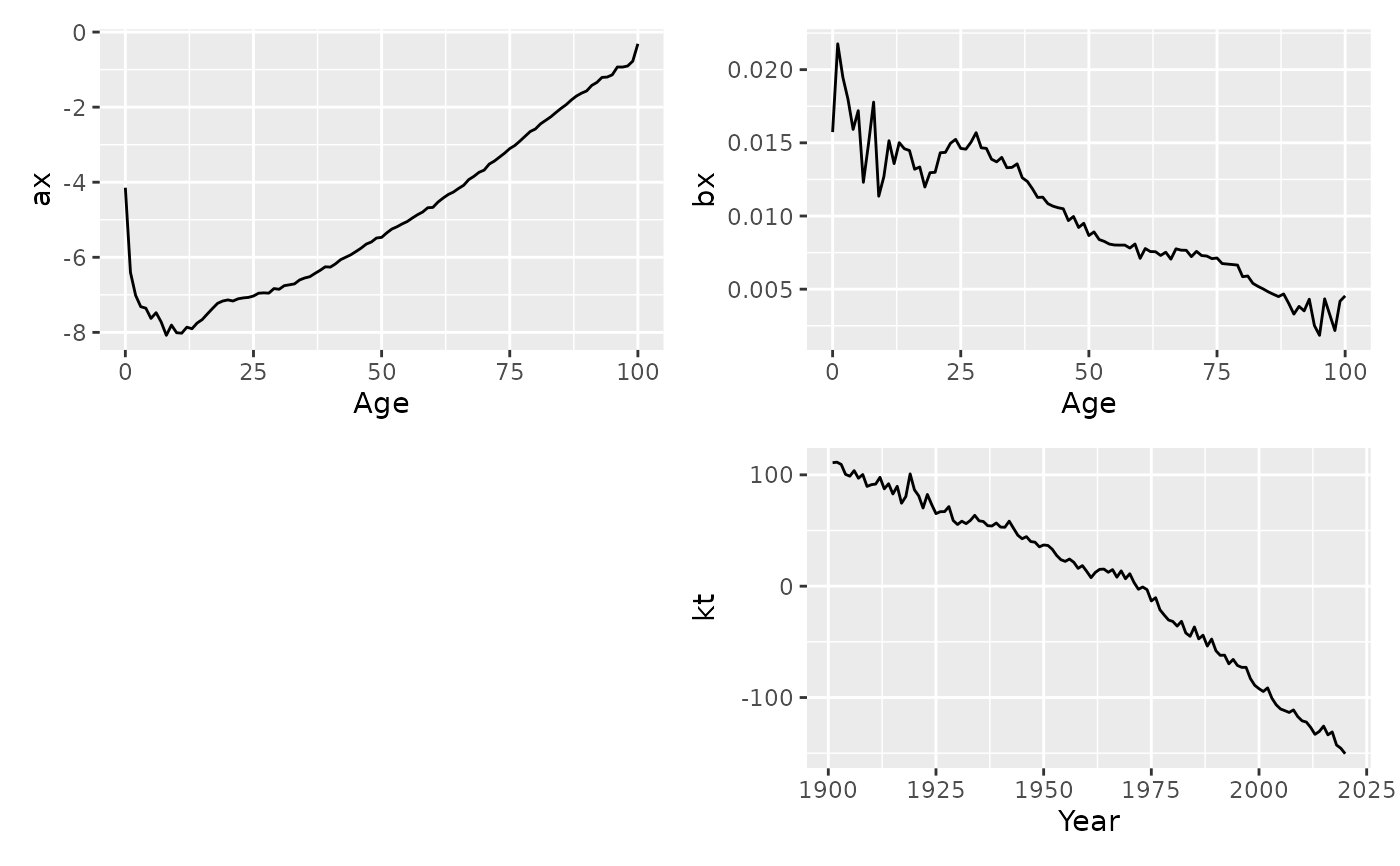
Lee-Carter model

Lee-Carter model of mortality or fertility rates. LC() returns a Lee-Carter model applied to the formula's response variable as a function of age. This produces a standard Lee-Carter model by default, although many other options are available. Missing rates are set to the geometric mean rate for the relevant age.

Usage

LC(
  formula,
  adjust = c("dt", "dxt", "e0", "none"),
  jump_choice = c("fit", "actual"),
  scale = FALSE,
  ...
)

Arguments

formula: Model specification. It should include the log of the variable to be modelled. See the examples.
adjust: method to use for adjustment of coefficients \(k_t\). Possibilities are "dt" (Lee-Carter method, the default), "dxt" (BMS method), "e0" (Lee-Miller method based on life expectancy) and "none".
jump_choice: Method used for computation of jump-off point for forecasts. Possibilities: "actual" (use actual rates from final year) and "fit" (use fitted rates). The original Lee-Carter method used "fit" (the default), but Lee and Miller (2001) and most other authors prefer "actual".
scale: If TRUE, bx and kt are rescaled so that kt has drift parameter = 1.
...: Not used.

Value

A model specification.

References

Basellini, U, Camarda, C G, and Booth, H (2022) Thirty years on: A review of the Lee-Carter method for forecasting mortality. International Journal of Forecasting, 39(3), 1033-1049.

Booth, H., Maindonald, J., and Smith, L. (2002) Applying Lee-Carter under conditions of variable mortality decline. Population Studies, 56, 325-336.

Lee, R D, and Carter, L R (1992) Modeling and forecasting US mortality. Journal of the American Statistical Association, 87, 659-671.

Lee R D, and Miller T (2001). Evaluating the performance of the Lee-Carter method for forecasting mortality. Demography, 38(4), 537–549.

Author

Rob J Hyndman

Examples

lc <- norway_mortality |>
  dplyr::filter(Sex == "Female") |>
  model(lee_carter = LC(log(Mortality)))
report(lc)
#> Series: Mortality 
#> Model: LC 
#> Transformation: log(Mortality) 
#> 
#> Options:
#>   Adjust method: dt
#>   Jump choice: fit
#> 
#> Age functions
#> # A tibble: 111 × 3
#>     Age    ax     bx
#>   <int> <dbl>  <dbl>
#> 1     0 -4.33 0.0152
#> 2     1 -6.16 0.0219
#> 3     2 -6.77 0.0189
#> 4     3 -7.14 0.0184
#> 5     4 -7.18 0.0162
#> # ℹ 106 more rows
#> 
#> Time coefficients
#> # A tsibble: 124 x 2 [1Y]
#>    Year    kt
#>   <int> <dbl>
#> 1  1900  117.
#> 2  1901  111.
#> 3  1902  105.
#> 4  1903  110.
#> 5  1904  108.
#> # ℹ 119 more rows
#> 
#> Time series model: RW w/ drift 
#> 
#> Variance explained: 64.85%
autoplot(lc)