k-fold Cross-Validation applied to an autoregressive model

CVar computes the errors obtained by applying an autoregressive modelling function to subsets of the time series y using k-fold cross-validation as described in Bergmeir, Hyndman and Koo (2015). It also applies a Ljung-Box test to the residuals. If this test is significant (see returned pvalue), there is serial correlation in the residuals and the model can be considered to be underfitting the data. In this case, the cross-validated errors can underestimate the generalization error and should not be used.

Usage

CVar(
  y,
  k = 10,
  FUN = nnetar,
  cvtrace = FALSE,
  blocked = FALSE,
  LBlags = 24,
  ...
)

Arguments

y

Univariate time series

k

Number of folds to use for cross-validation.

FUN

Function to fit an autoregressive model. Currently, it only works with the nnetar function.

cvtrace

Provide progress information.

blocked

choose folds randomly or as blocks?

LBlags

lags for the Ljung-Box test, defaults to 24, for yearly series can be set to 20

...

Other arguments are passed to FUN.

Value

A list containing information about the model and accuracy for each fold, plus other summary information computed across folds.

References

Bergmeir, C., Hyndman, R.J., Koo, B. (2018) A note on the validity of cross-validation for evaluating time series prediction. Computational Statistics & Data Analysis, 120, 70-83. https://robjhyndman.com/publications/cv-time-series/.

See also

CV, tsCV.

Author

Gabriel Caceres and Rob J Hyndman

Examples

modelcv <- CVar(lynx, k=5, lambda=0.15)
print(modelcv)
#> Series: lynx 
#> Call:   CVar(y = lynx, k = 5, lambda = 0.15)
#> 
#> 5-fold cross-validation
#>                  Mean          SD
#> ME        -61.7601138 336.0087913
#> RMSE      962.3500615 342.0693318
#> MAE       629.6217966 229.9652825
#> MPE       -18.6537928  15.6268659
#> MAPE       53.8705735  11.9655705
#> ACF1        0.1697009   0.2299590
#> Theil's U   0.8666704   0.1953902
#> 
#> p-value of Ljung-Box test of residuals is  0.4510229 
#> if this value is significant (<0.05),
#> the result of the cross-validation should not be used
#> as the model is underfitting the data.
print(modelcv$fold1)
#> $model
#> Series: y 
#> Model:  NNAR(11,6) 
#> Call:   FUN(y = y, lambda = 0.15, subset = trainset)
#> 
#> Average of 20 networks, each of which is
#> a 11-6-1 network with 79 weights
#> options were - linear output units 
#> 
#> sigma^2 estimated as 0.07838
#> 
#> $accuracy
#>                 ME     RMSE      MAE       MPE     MAPE       ACF1 Theil's U
#> Test set -4.287465 838.5006 483.9661 -3.953391 51.16217 -0.1048098 0.6609429
#> 
#> $testfit
#> Time Series:
#> Start = 1821 
#> End = 1934 
#> Frequency = 1 
#>   [1]         NA         NA         NA         NA         NA         NA
#>   [7]         NA         NA         NA         NA         NA  114.88005
#>  [13]  161.67031  299.99623  577.63133 2251.69300 2777.49689 3393.08619
#>  [19] 1947.11849  411.48374  159.20947   47.39196   67.71385  210.33139
#>  [25]  548.16300 1042.23818 2101.56383 2555.71266  951.68341  360.03759
#>  [31]  177.44979  255.43826  219.79217  953.69969 1586.33932 2833.98853
#>  [37] 2957.66280 2160.89483  718.89174  284.15376  251.63173  229.93529
#>  [43]  528.32011 1590.37655 3217.43455 3769.53585 4154.35548 1515.27075
#>  [49]  220.23811  422.76476  363.60317  805.55365 1643.61844 1723.74430
#>  [55] 2340.12520 1444.08252  527.16194  288.17935  106.80893  219.68341
#>  [61]  443.55591 1005.80080 1053.34109 2879.30256 4359.76615 2587.65542
#>  [67]  385.83821  189.95960   87.06765   51.32500   66.62722  190.31618
#>  [73]  952.80904 1326.77443 3930.89083 3441.74357 2404.53343  105.31667
#>  [79]  155.46760  379.56735  763.49398 1318.84411 3329.13879 6834.73921
#>  [85] 6413.63937 3777.99387 1804.79778  361.35506  359.77234  779.64371
#>  [91] 1330.91545 2728.45865 3605.71537 3540.38137 2887.53368 3708.91225
#>  [97]  685.67440   86.43151  106.37469  109.41606  222.55274  713.39860
#> [103] 1137.22354 2439.92397 3451.65321 2836.75449 1540.68410  727.69908
#> [109]  446.42198  471.73105  701.27828 1623.25263 2655.03288 3352.86223
#> 
#> $testset
#>  [1]   1  10  15  31  33  34  46  48  49  57  59  62  63  68  69  73  77  94  99
#> [20] 102 108 110 111
#> 

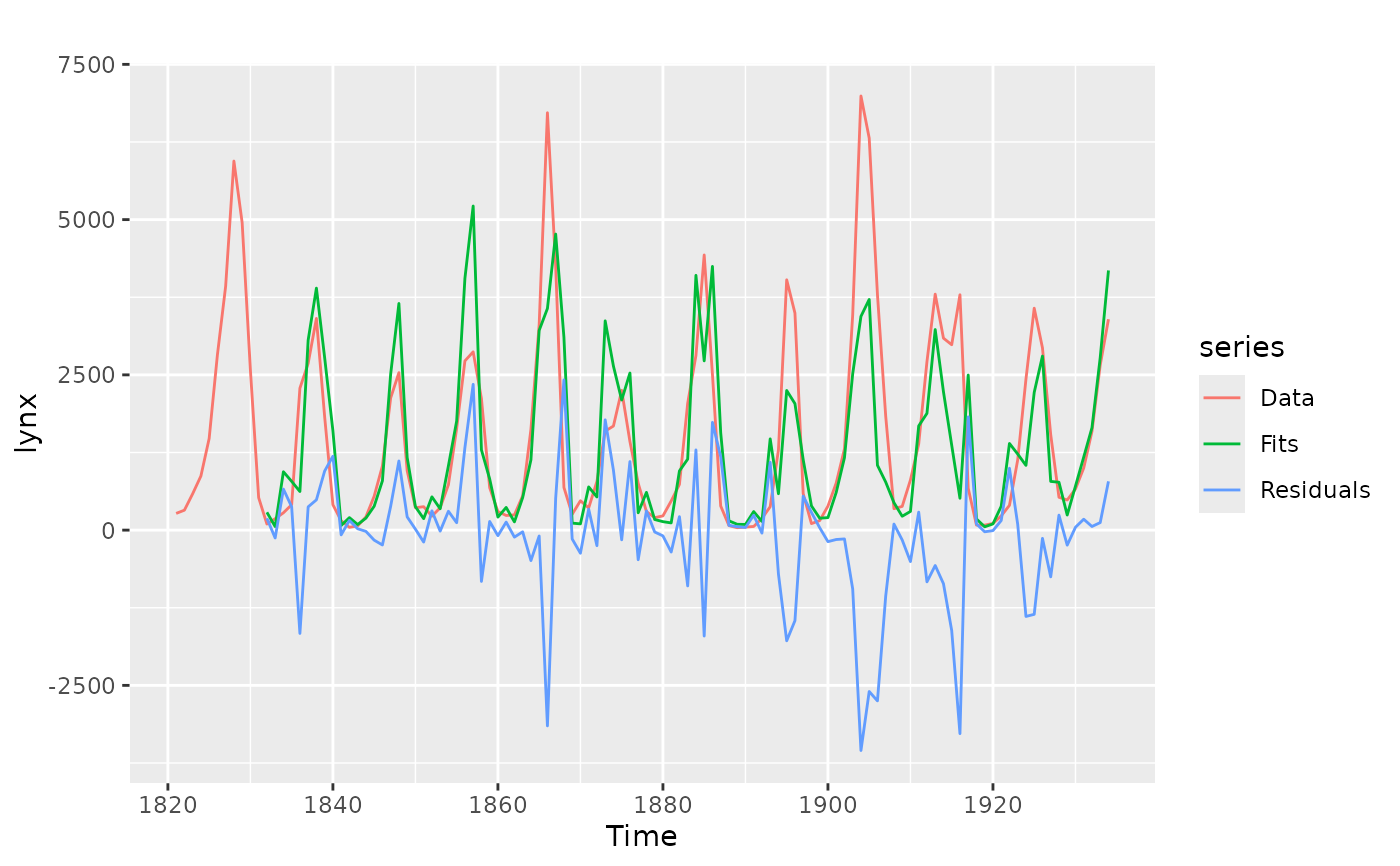
library(ggplot2)
autoplot(lynx, series="Data") +
  autolayer(modelcv$testfit, series="Fits") +
  autolayer(modelcv$residuals, series="Residuals")
#> Warning: Removed 11 rows containing missing values or values outside the scale range
#> (`geom_line()`).
#> Warning: Removed 11 rows containing missing values or values outside the scale range
#> (`geom_line()`).

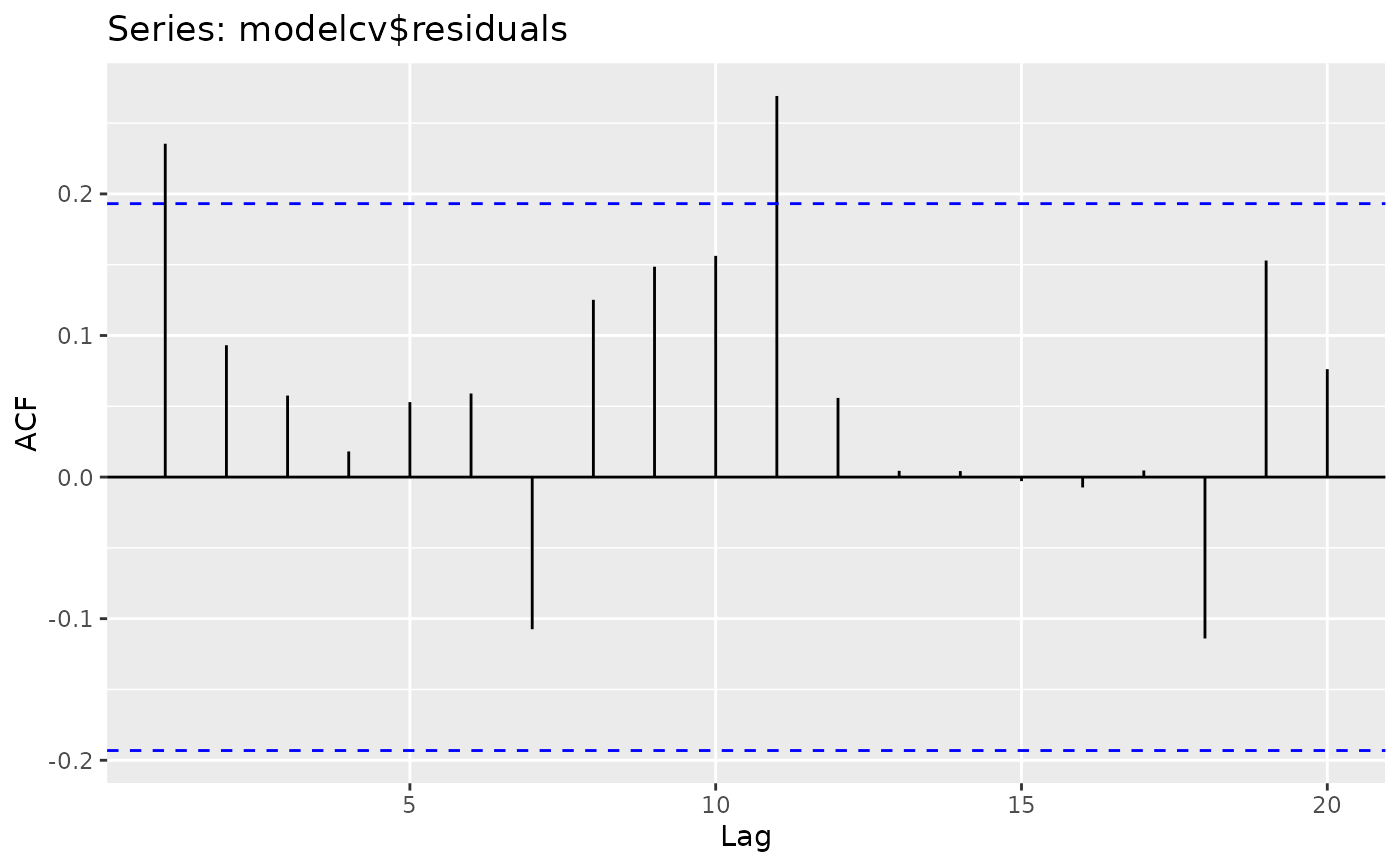
ggAcf(modelcv$residuals)