Functional demographic model

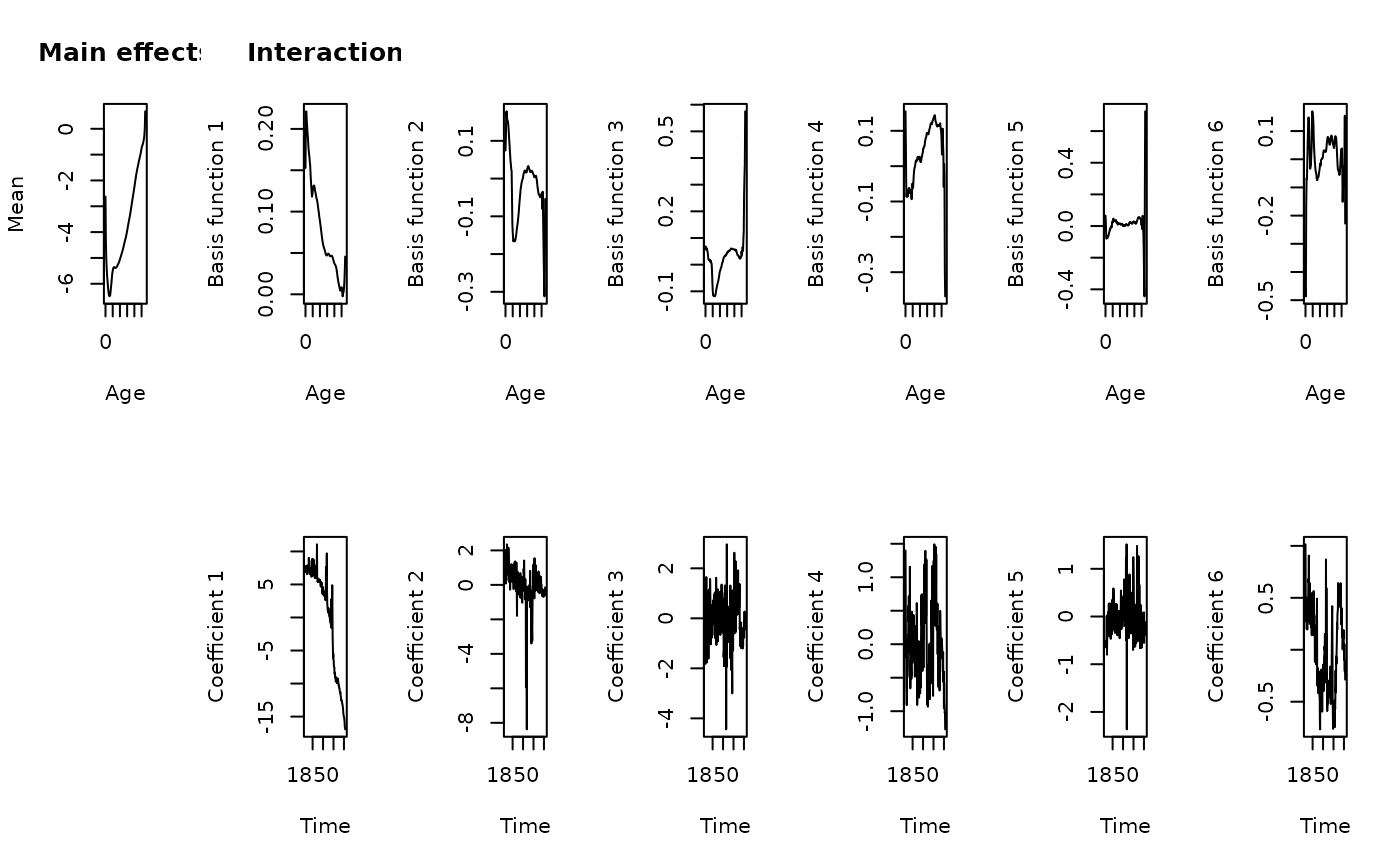
Fits a basis function model to demographic data. The function uses optimal orthonormal basis functions obtained from a principal components decomposition.

Usage

fdm(
  data,
  series = names(data$rate)[1],
  order = 6,
  ages = data$age,
  max.age = max(ages),
  method = c("classical", "M", "rapca"),
  lambda = 3,
  mean = TRUE,
  level = FALSE,
  transform = TRUE,
  ...
)

Arguments

data: demogdata object. Output from read.demogdata.
series: name of series within data holding rates (1x1).
order: Number of basis functions to fit.
ages: Ages to include in fit.
max.age: Maximum age to fit. Ages beyond this are collapsed into the upper age group.
method: Method to use for principal components decomposition. Possibilities are “M”, “rapca” and “classical”. See ftsm for details.
lambda: Tuning parameter for robustness when method="M".
mean: If TRUE, will estimate mean term in the model before computing basis terms. If FALSE, the mean term is assumed to be zero.
level: If TRUE, will include an additional (intercept) term that depends on the year but not on ages.
transform: If TRUE, the data are transformed with a Box-Cox transformation before the model is fitted.
...: Extra arguments passed to ftsm.

Value

Object of class “fdm” with the following components:

label: Name of country
age: Ages from data object.
year: Years from data object.
<series>: Matrix of demographic data as contained in data. It takes the name given by the series argument.
fitted: Matrix of fitted values.
residuals: Residuals (difference between observed and fitted).
basis: Matrix of basis functions evaluated at each age level (one column for each basis function). The first column is the fitted mean.
coeffs: Matrix of coefficients (one column for each coefficient series). The first column are all ones.
mean.se: Standard errors for the estimated mean function.
varprop: Proportion of variation explained by each basis function.
weights: Weight associated with each time period.
v: Measure of variation for each time period.
type: Data type (mortality, fertility, etc.)
y: The data stored as a functional time series object.

References

Hyndman, R.J., and Ullah, S. (2007) Robust forecasting of mortality and fertility rates: a functional data approach. Computational Statistics & Data Analysis, 51, 4942-4956. https://robjhyndman.com/publications/funcfor/

Author

Rob J Hyndman

Examples

france.fit <- fdm(fr.mort)
summary(france.fit)
#> Functional demographic model
#> 
#> Call: fdm(data = fr.mort) 
#> 
#> Region: FRATNP
#> Data type: mortality
#> Years in fit: 1816 - 2006
#> Ages in fit: 0 - 110 
#> 
#> Order: 6
#> Percentage variation due to basis functions: 93.8% 2.3% 1.6% 0.6% 0.4% 0.3%
#> 
#> Averages across ages:
#>       ME      MSE      MPE     MAPE 
#> -0.09913  0.05686     -Inf      Inf 
#> 
#> Averages across years:
#>       IE      ISE      IPE     IAPE 
#>  0.45441  0.73512 -1.66272  8.08544 
#> 
plot(france.fit)

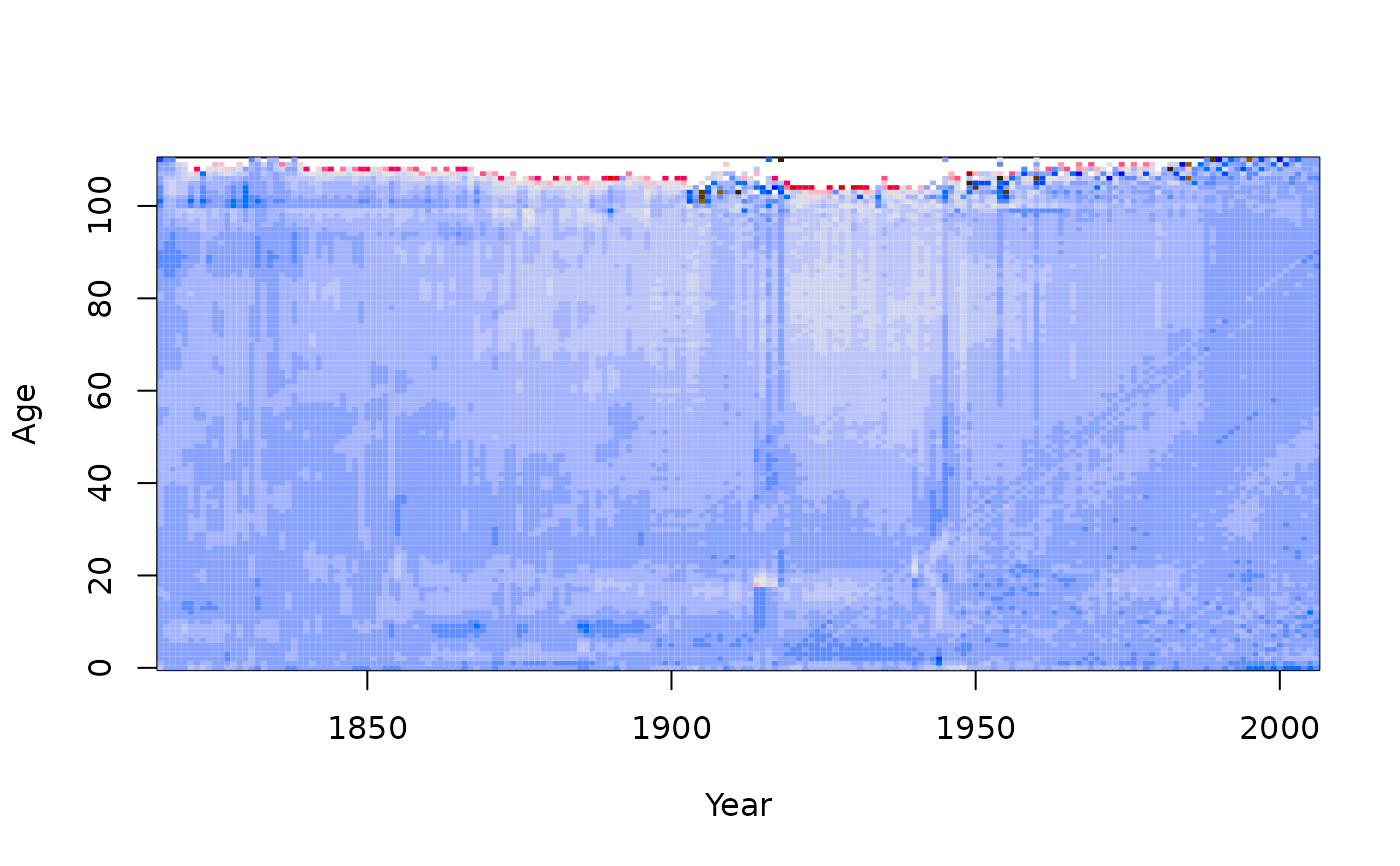
plot(residuals(france.fit))