Cubic Spline Forecast

Returns local linear forecasts and prediction intervals using cubic smoothing splines.

Usage

splinef(
  y,
  h = 10,
  level = c(80, 95),
  fan = FALSE,
  lambda = NULL,
  biasadj = FALSE,
  method = c("gcv", "mle"),
  x = y
)

Arguments

y: a numeric vector or time series of class ts
h: Number of periods for forecasting
level: Confidence level for prediction intervals.
fan: If TRUE, level is set to seq(51,99,by=3). This is suitable for fan plots.
lambda: Box-Cox transformation parameter. If lambda="auto", then a transformation is automatically selected using BoxCox.lambda. The transformation is ignored if NULL. Otherwise, data transformed before model is estimated.
biasadj: Use adjusted back-transformed mean for Box-Cox transformations. If transformed data is used to produce forecasts and fitted values, a regular back transformation will result in median forecasts. If biasadj is TRUE, an adjustment will be made to produce mean forecasts and fitted values.
method: Method for selecting the smoothing parameter. If method="gcv", the generalized cross-validation method from smooth.spline is used. If method="mle", the maximum likelihood method from Hyndman et al (2002) is used.
x: Deprecated. Included for backwards compatibility.

Value

An object of class "forecast".

The function summary is used to obtain and print a summary of the results, while the function plot produces a plot of the forecasts and prediction intervals.

The generic accessor functions fitted.values and residuals

extract useful features of the value returned by splinef.

An object of class "forecast" containing the following elements:

model: A list containing information about the fitted model
method: The name of the forecasting method as a character string
mean: Point forecasts as a time series
lower: Lower limits for prediction intervals
upper: Upper limits for prediction intervals
level: The confidence values associated with the prediction intervals
x: The original time series (either object itself or the time series used to create the model stored as object).
onestepf: One-step forecasts from the fitted model.
fitted: Smooth estimates of the fitted trend using all data.
residuals: Residuals from the fitted model. That is x minus one-step forecasts.

Details

The cubic smoothing spline model is equivalent to an ARIMA(0,2,2) model but with a restricted parameter space. The advantage of the spline model over the full ARIMA model is that it provides a smooth historical trend as well as a linear forecast function. Hyndman, King, Pitrun, and Billah (2002) show that the forecast performance of the method is hardly affected by the restricted parameter space.

References

Hyndman, King, Pitrun and Billah (2005) Local linear forecasts using cubic smoothing splines. Australian and New Zealand Journal of Statistics, 47(1), 87-99. https://robjhyndman.com/publications/splinefcast/.

Author

Rob J Hyndman

Examples

fcast <- splinef(uspop,h=5)
plot(fcast)

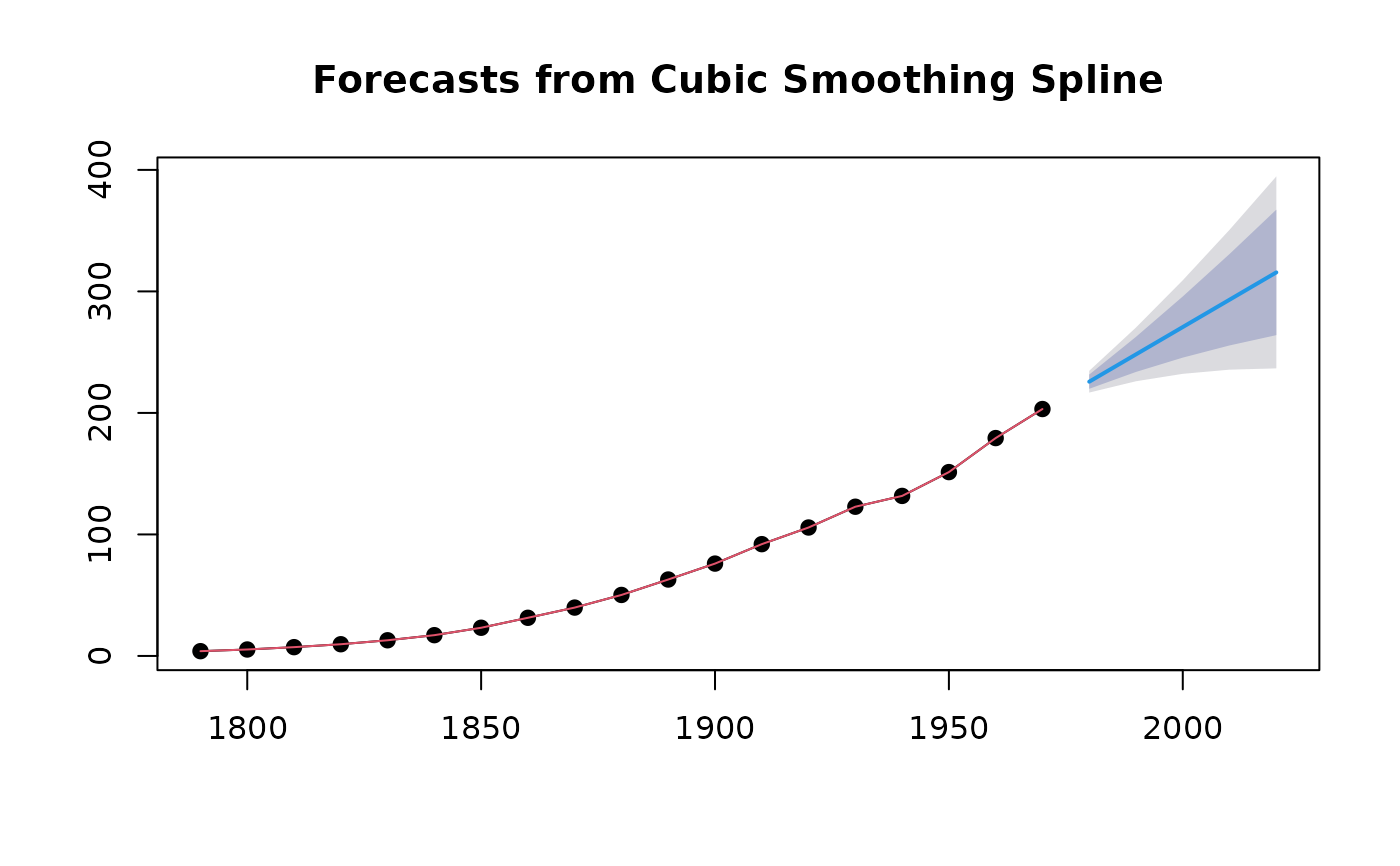summary(fcast)
#> 
#> Forecast method: Cubic Smoothing Spline
#> 
#> Model Information:
#> $beta
#> [1] 0.0006859
#> 
#> $call
#> splinef(y = uspop, h = 5)
#> 
#> 
#> Error measures:
#>                     ME     RMSE      MAE        MPE     MAPE       MASE
#> Training set 0.7704553 4.572546 3.165298 -0.6110405 8.174722 0.04536795
#>                    ACF1
#> Training set -0.4363661
#> 
#> Forecasts:
#>      Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
#> 1980       225.6937 219.8454 231.5419 216.7496 234.6378
#> 1990       248.1814 233.7246 262.6382 226.0717 270.2912
#> 2000       270.6692 245.5023 295.8361 232.1798 309.1586
#> 2010       293.1569 255.5241 330.7897 235.6025 350.7113
#> 2020       315.6447 264.0068 367.2826 236.6713 394.6181